第2回：モンテカルロ木探索

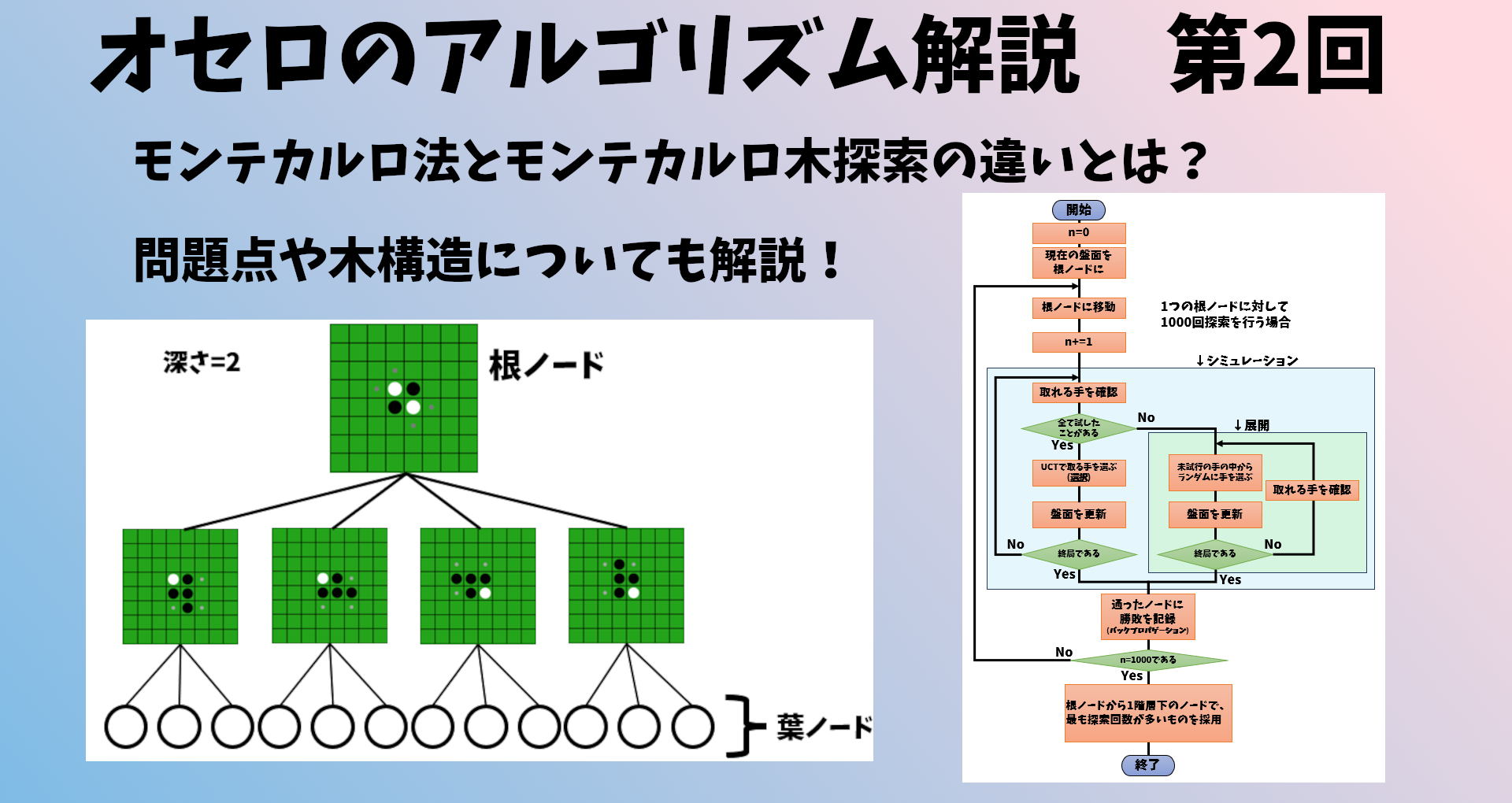
この記事では、前回説明を省略した「モンテカルロ木探索」の詳細や、探索アルゴリズムにおける「木」の概念、「モンテカルロ法」の問題点などを絡めて解説します。

前回の記事はこちらからどうぞ

1.モンテカルロ法の問題点

基本的にモンテカルロ法では、着手可能手にそれぞれn回の試行を行う方式をとります。そのため、中盤の選択肢が膨らむ局面では試行回数が多くなり処理時間が長くなってしまうという問題があります。
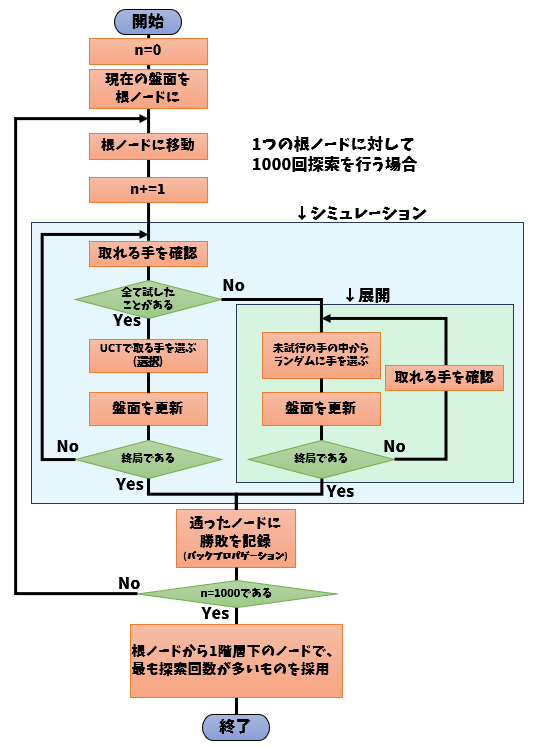
その問題を解決する手法がモンテカルロ木探索です。この手法の特徴を一言で説明すると、「勝てそうな手を優先して試行する」というものです。もう少し具体的な流れを説明すると、

最初は全ての手を平等に試す
試行を重ねていくうちに、勝率が高そうな手が見えてきたら、そちらを多めに試す
ただし、初期の勝率はまだ不確かなので、他の手も試す（探索の幅を残す）

です。
このようにして、“手の評価”と“試行回数の配分”を同時に最適化していくのがモンテカルロ木探索の基本的な考え方です。この手法では一定量の試行回数を効率的に割り振ることができるため、はやい速度を保つことが可能です。

2.木構造とは

モンテカルロ「木」探索という名前にもある通り、この手法では「木構造（ツリー構造）」という形を使って、探索の過程を整理・管理しています。
そもそも木構造とは、1つの親ノードから複数の子ノードが枝分かれする構造のことを指します。これは、ゲームの先読み（探索）と非常に相性が良いのです。
例えばオセロで、ある1手目の後に取りうる選択肢が複数あり、さらにその後の2手目の選択肢も複数存在して、3手目...というように、1手ごとに分岐が広がっている構造を想像してみてください。このとき、
それぞれの盤面を「ノード」として表し、
そこから可能な次の手を枝分かれさせていく
という形で整理するのが「木構造」です。
この図のように、根元から枝分かれしていく様を木に例えてこう呼ばれているわけです。また、一番上にくるノードは「根ノード」、一番下の、それ以上分岐がないノードを「葉ノード」と表したりします。

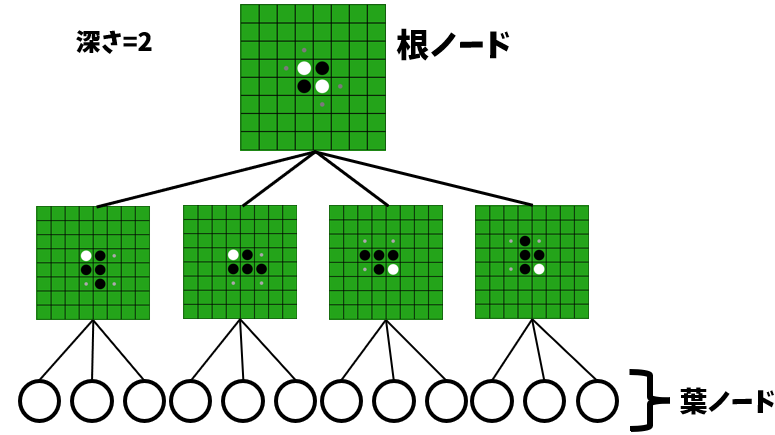
木構造のつくりを説明する画像。一番上に「根ノード」として、オセロの初期盤面が書いてあり、そこから下に枝分かれする形で黒が取れる4つの手を取った場合の盤面が繋がっている。また、その4つの盤面から下方向にそれぞれ3つの丸が、「葉ノード」として枝分かれして繋がっている。この図は深さが2なので、丸の部分が葉ノードとなっている。

この考え方はオセロに限らず、探索アルゴリズム系では非常によく用いられます。
木構造で管理する事によって、

どの手をどれだけ試したか
その手の勝率がどれくらいか

といった情報をノードごとに保持、更新することができます。
これにより、モンテカルロ木探索では「よく勝てる手の枝を深く掘る」といった効率的な探索が可能になるのです。

備考

この「木構造」は次回紹介するminimax法などでも活用されています。次回は、モンテカルロ木探索とminimax法での木構造の扱い方の違いにも触れていく予定です。

3.モンテカルロ木探索の詳細

さて、先ほど

最初は全ての手を平等に試す
試行を重ねていくうちに、勝率が高そうな手が見えてきたら、そちらを多めに試す
ただし、初期の勝率はまだ不確かなので、他の手も試す（探索の幅を残す）

と述べましたが、この後半の2点は決められた回数の中で「より一つの手に集中することで勝率を正確に求めたい」一方、「なるべく他の手も試して意外と強い手を見逃さないようにしたい」という矛盾を抱えているのです。
この相反する二つをどのように両立させたら良いでしょうか？
順を追って説明していきます。

まずは全ての手を試す

この部分はなんとなく想像できるかもしれません。そのままです。
まだ試していないノードが存在したら、それを一通り試します。こうすることで、そのノードから着手できる全ての手を少なくとも1回ずつ試したという状況を作ることができます。
具体的には、根ノードから取れる試したことのない手(ノード)を一つ選んだあと、そこから対局が終わるまでランダムに局面を進めます。(シミュレーション)この勝敗をシュミレーション中に通った各ノードに保存する(バックプロパゲーション)ことで、その手と勝敗の関係が統計的に蓄積されていくことになります。
また、この未探索のノードをランダムにシミュレーションすることを「展開」と呼びます。

優先順位をつける

すべての手(子ノード)が最低1回ずつ試されているノードの場合は、優先順位をつけて最も優先順位が高いものを試していきます。(選択)
この優先順位は、

勝率が高い手
試行回数が足りない手

をもとに一定の決まりに沿って決定します。ここの難しい点は、その何回かのシミュレーションの結果による各ノードの既知の勝率利用(知識活用)と、シミュレーションの回数の不足による探索のバランスを取ることであり、また、この決定方法は無数に存在するため、「どの数式を使うのか」という問題も出てきます。
ここでは、比較的シンプルなUCT(Upper Confidence Tree)の数式を紹介します。
数式は、

\frac{w}{n} + c \sqrt{\frac{\ln N}{n}}

と表され、文字の意味は

w:そのノードを経由して勝った回数
n:そのノードの試行回数
N:そのノードの親ノードの試行回数（親が選ばれた回数）
c:定数。知識活用と、探索のバランスを決めるパラメータで、理論上は $\sqrt{2}$ だが、運用時は探索がうまくいくように調整する。

です。
左の項はそのノードの勝率、右の項はそのノードの「選ばれていなさ」で、試行回数が少ないほど値が大きくなります。また、そこにcをかけることで探索の重要度を決定しています。
このUCTは、

よく試されていて勝率が高い手 → 点数が高くなる
試行回数が少ない手 → まだチャンスがあると判断される(点数が高くなる)
たくさん試されていて勝率も悪い手 → 点数が下がる

といった特徴があり、「すべてのノードに関してこの計算を行い、最も数字が大きいノードでシミュレーションを進める。」というのを繰り返すことで、最終的には「勝てそうな手」へと試行が収束していくのです。

最終的な決定

このようにして1つの根ノードで、決められた量の試行を行い、「最も勝てそうな手」を選びます。ここで重要なのは、選ぶノードは「最も勝率が高い手」ではなく、「最も試行回数が多い手」のノードであるということです。
これは、例えば

試行回数が10回で、勝利数が5回(勝率50%)
試行回数が1000回で、勝利数が499回(勝率49.9%)

の2つの手があった場合、一見すると前者のほうが勝率は高いように見えますが、試行数が少ないため偶然の可能性もあります。
一方、後者は非常に多く試されており、信頼性の高い勝率と判断できます。モンテカルロ木探索では、試行が集中した=信頼されている手と考え、最も試行回数の多いノードを最終手として選ぶのです。

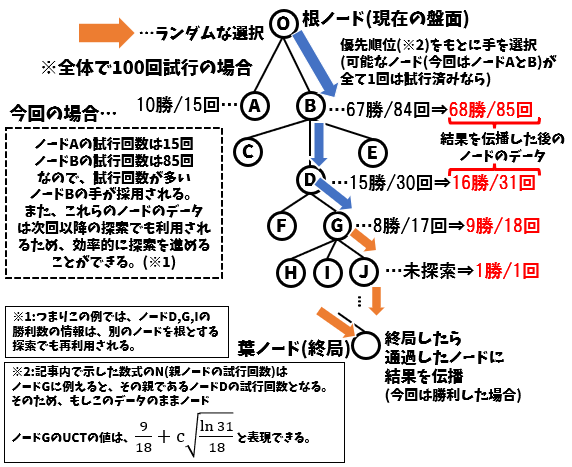
※上図のノードGの子ノードは、ノードH,I,Jの他にもあり、合計で18個以上あると思ってください。

4.おわりに

この記事では、モンテカルロ木探索について詳しく解説してきました。次回は、前回紹介した「minimax法」に関して、モンテカルロ木探索との違いも絡めつつ解説します。

次の記事↓

この記事は最新です

前回の記事↓

オセロのアルゴリズムに関して