オセロのアルゴリズムに関して

e_Coach_AIはオセロのアルゴリズムを用いてオセロのコーチングを行ってくれるソフトウェアです。
ですが、「オセロのアルゴリズム」と言っても様々な手法が存在します。
そこで、本サイトでは全4回に分けて、

• オセロのアルゴリズムにはどんなものがあるのか
• モンテカルロ木探索
• minimax探索など
• 評価関数の工夫

のテーマで解説していきます。
また、この記事ではプログラミングの実装例は示さず、言葉と図を用いて、考え方ベースで説明していく方針を取りたいと思います。

第1回：オセロのアルゴリズムにはどんなものがあるのか

この記事では、そもそもアルゴリズムとは何なのか、AIとの関係、そして、多数ある中から一部を取り上げてオセロのアルゴリズムを紹介していきます。

1.アルゴリズムとは

そもそも、アルゴリズムとは何でしょうか？
普段生活していたら時々耳にすることもあるかもしれません。
アルゴリズムとは、「コンピュータが問題を解くための計算方法」のことを指します。
もっと簡単に言うと、「問題の解き方」です。
ある状況や入力に対して、そのアルゴリズムで定められた計算を行うと毎回一定の決まった結果が得られるというものです。

ここで、「5×3+5×397」を計算することを想像してみてください。
この程度の計算では単純にに頭から計算して、
15+1985=2000
のように求めることもできるかもしれませんが、5を共通因数としてくくると、
5×400=2000
のようにより容易に計算ができるようになると思いませんか？
アルゴリズムでも同じです。(例に出した計算は人間に分かりやすくするためのものであり、コンピュータではあまり差は出ないと思いますが。) 同じ入力で、求める結果が同じでも、その過程を工夫する事によって大幅に計算時間や消費メモリなどを節約できる可能性があるのです。 そのため、世の中には目的が同じでも多様な過程を踏む異なったアルゴリズムがたくさん存在します。

アルゴリズムの例

有名なアルゴリズムの例として、「並び替え(ソート)」が挙げられます。
不規則な並びをした複数の数字を昇順に並び替える処理のことで、

• バブルソート(簡単だが遅い)
• バ選択ソート
• クイックソート(速い)
• マージソート(安定して速い)

など複数の有名なアルゴリズムが存在しますが、これらは目的こそ同じですが、処理速度や効率は異なります。
いかに効率的に目標を得ることができるかは、この「アルゴリズム」の性能次第なのです。

2.アルゴリズムとAIの関係

特に最近、AIという言葉をよく耳にするようになっているのではないでしょうか？
実は、AIとアルゴリズムは密接に関係していますが、別物として扱われます。

AIとは

まずAIとは、「人間のように学習し、判断する仕組み全体」を意味します。
画像を見て「これは猫だ」と判断したり、文章を読んで「こう返そう」と考えたり、そんなふうに知的な処理を行うのがAIです。

アルゴリズムはAIの部品

AIの内部では、実に多くのアルゴリズムが使われています。

• データからパターンを学習する 学習アルゴリズム
• 入力に対して最適な出力を選ぶ 推論アルゴリズム
• 効率を高めるための 最適化アルゴリズム

など、AIはこうしたアルゴリズムを組み合わせて、知的な判断を可能にしているのです。

3.オセロのアルゴリズム

ここまではアルゴリズムの言葉の意味や役割を解説してきましたが、ここからは具体的にオセロのアルゴリズムについて解説していきます。
今回はざっくりとした概要のみ解説します。

モンテカルロ法/モンテカルロ木探索

これらは名前は似ているものの微妙に異なるのですが、その詳しい解説は次回行うことにし、簡単な仕組みだけを解説します。
モンテカルロ法とは、「ランダムな試行を繰り返し行い、答えを導く」という手法です。有名なものだと「円周率をランダムな点の分布から近似する」といったものがが挙げられます。(ここでは踏み込んだ説明はしません。気になる方はぜひご自身で調べてみてください。)
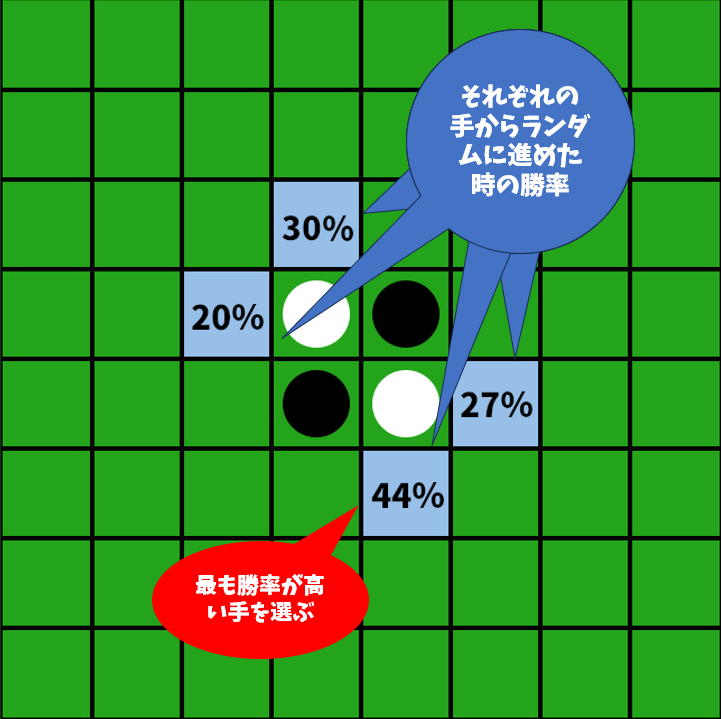
オセロでは、

• 1.現在の盤面における可能な手を一つ選ぶ
• 2.その盤面から、勝敗がつくまでランダムに対局を進める
• 3.これを何度も繰り返し、勝率を測る

このようにして、その手の中で最も勝率が高い手を選ぶというものです。この手法は試行回数が多いほどより正確になりますが、その分試行回数が増えるので処理時間は長くなってしまうという特徴があります。また、モンテカルロ木探索はその処理がもう少し効率的になるように工夫された手法なのです。

minimax法/negamax法/alpha-beta法/nega-alpha法

これら4つのアルゴリズムは、根本的には「『相手も自分も最善を尽くす』という前提のもと、先読みして最善手を探す」という共通の考え方に基づいています。
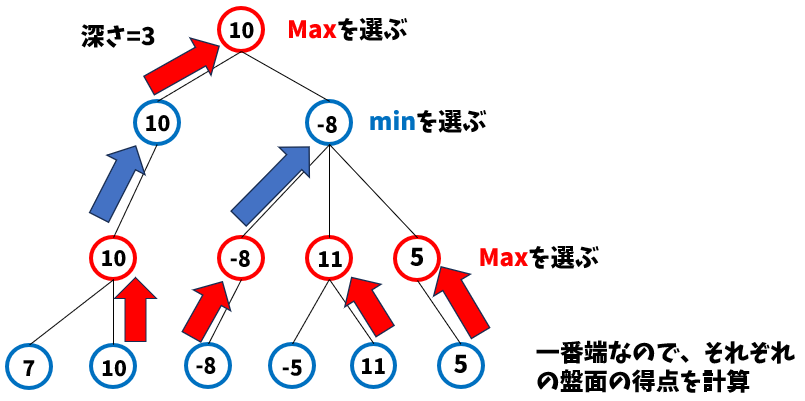
具体的には、

• 自分の手番では最も得点(後述)が高い手(自分に有利な手)を選ぶ
• 相手の手番では最も得点が低い手(相手に有利な手)を選ぶ

これを交互に繰り返して、最終的に「最も点数の高い手」を選ぶといった流れです。たとえば3手先まで読むとき、自分→相手→自分の目線から交互に評価し、「最終的に自分がどの手を選ぶべきか」を逆算して決めます。また、この深さが大きいほどアルゴリズムも強くなりますが、計算に時間がかかるようになってしまいます。
では、これら4つの違いは何でしょうか？

minimax法は今解説したことをただ繰り返すだけで、実装自体は最も単純です。しかし、これは指定された深さ(何手先まで読むか)で取りうる盤面全てを計算して比較することになるので、計算に膨大な時間がかかってしまうという欠点があります。

negamax法は上記の実装を改良してシンプルに記述(プログラミング)することができるようにされたものです。具体的には、minimax法では自分の手番か相手の手番かどうかによって選ぶ値を場合分けする必要があったのですが、この手法では相手の手番の時に得点の正負を反転させることで常に最大の得点を選ぶだけでいいようになります。そのため、実装はシンプルになるのですが、処理速度はminimax法と変りません。

alpha-beta法はminimax法に「枝刈り」の仕組みを加えたものです。「良くない手」の探索を打ち切る(枝刈り)ことで探索量を減らすことができるため、minimax法から大幅に高速化することができるようになっています。(詳細は第3回で)

nega-alpha法は、名前からもなとなく察することができますが、negamax法とalpha-beta法の両方を組み合わせた手法で、処理速度が速いうえにコーディングがシンプルになるのです。

このように、この4つの手法はすべてminimax法をベースとしつつ、処理速度や実装のしやすさの面で段階的に改良されたものなのです。そのため、帰ってくる結果はどの手法でも同じになります。

ここで、先ほどから時々登場している「得点」という言葉についても解説します。
本来、オセロには「得点」という概念はありません。しかし、盤面どうしを比較して「どちらが有利か」を判断するためには、何らかの基準が必要になります。
そのために導入されるのが評価関数です。評価関数とは、ある盤面に対して「どれだけ有利か」を数値で表す仕組みのことです。これにより、AIは「この手を打てば評価値が上がる」「こっちの手は不利だ」といった判断が可能になります。そして、評価関数がいかに正確に状況を判断できるかがアルゴリズム全体の“強さ”に直結するのです。

4.おわりに

というわけで今回はアルゴリズムの意味、AIとアルゴリズムの関係、具体的なオセロのアルゴリズムを紹介しました。
次回は、先ほど詳細を省略した「モンテカルロ木探索」について詳しく解説します。

次の記事↓

前回の記事↓